分布近似问题
就本人目前所了解的现状,分布近似问题尚未在学界被严肃定义,多数研究者可能熟悉的是多年来持续火热的生成模型:生成对抗网络(Generative Adversarial Networks, GAN),扩散模型(Diffusion Model)等等。另一些核心却冷门的领域,如马尔科夫链蒙特卡洛采样(Markov Chain Monte Carlo, MCMC),或是变分推理(Variational Inference, VI),则极少成为人们热议的对象。实际上,MCMC与VI常常出现在生成模型的论文中,从远古时期的变分自编码器VAE,到Energy-based、基于Score Matching的生成模型,再到近两年火热的扩散模型(Diffusion Model),甚至生成对抗网络(GAN)都可以被解释为使用特殊kernel的VI。另一方面,起始于2016年的粒子变分推理法(Particle-based Variational Inference, ParVI)被逐步构建与MCMC、VI方法的联系,生成与采样逐渐被统一理解为求解分布近似问题。
问题定义
什么是分布近似问题呢?该问题可被定义为如下形式:
\[ \min_{\mu} \mathcal{F}(\mu, \nu), \tag{1} \]
这里的\(\mu\)和\(\nu\)表示概率分布,\(\mathcal{F}\)表示一个度量,计算分布\(\mu\)和\(\nu\)之间的差异(不一定是距离),比如常见的KL散度(Kullback-Leibler Divergence),不常见的最大平均差异(Maximum Mean Discrepancy, MMD)和沃瑟斯坦距离(Wasserstein Distance)。
公式\((1)\)定义了一个优化问题,优化目标是\(\mathcal{F}(\cdot, \nu)\),或者写成\(\mathcal{F}_{\nu}\),优化变量是一个分布\(\mu\) , 全局最优为另一个分布 \(\nu\) 。也就是说,我们希望找到一个分布\(\mu\)在度量\(\mathcal{F}\)为判别标准的情况下接近分布\(\nu\)。
看起来,这个形式\((1)\)非常接近我们熟知的实向量空间中的优化(熟悉凸优化的读者应该能很快get到联系):
\[ \min_{x} F(x). \tag{2} \]
比如在深度学习领域,优化目标\(F\)表示训练的损失函数, 优化变量\(x\)表示神经网络的参数。当然,神经网络的参数是逐层的,但是我们可以将其抽象表示为一个高纬度向量。此外,由于训练过程中输入的数据(集)不计算梯度,所以可以不把这些变量表示在公式\((2)\)中。实际上在上述的表达中,数据集和网络结构共同定义了优化目标\(F\)。
看起来,公式\((1)\)可类比作公式\((2)\)的“升级”形式:
- 优化目标\(F\)计算两个向量之间的差异\(\to\)优化目标\(\mathcal{F}\)计算两个分布之间的差异。
- 优化变量\(x\)是一个实向量\(\to\)优化变量\(\mu\)是一个概率分布。
贝叶斯学习
那么表达式\((1)\)也可以按照上述神经网络的方式来理解吗?
实际上,如果从训练神经网络的角度阐释\((1)\), 我们可以非常方便地理解贝叶斯学习。首先回顾贝叶斯学习的基础——贝叶斯公式,建模了后验、似然、先验之间的关系:
\[ p(x|y) = \frac{p(y|x)p(x)}{p(y)}. \]
假设现在使用贝叶斯公式建模一个分类任务的神经网络参数\(x\)的后验分布,则有:
\[ p(x|\mathcal{D}_{train}) = \frac{p(\mathcal{D}_{train}|x)p(x)}{p(\mathcal{D}_{train})}, \]
这里使用\(\mathcal{D}_{train} = \{d_{train, j}\}^N_{j=1}\)表示训练数据集(为了表达简洁就不再拆分为输入和输出了),上述公式可进一步表达为:
\[ p(x| \mathcal{D}_{train} ) \propto \prod^N_{j=1}{p( d_{train, j} |x)}p(x), \tag{3} \]
上式表达了在给定训练数据集的情况下,神经网络参数的后验分布,可以被建模为每一条输入数据的似然函数的乘积,再乘上模型参数的先验分布\(p(x)\)。通常似然函数的形式比较复杂(由神经网络决定),先验分布形式简单,例如高斯分布。再推导一步,可得:
\[ -\log{p(x|\mathcal{D}_{train})} = -\left(\sum^{N}_{j=1}\log{p(d_{train, j}|x)} + \log{p(x)}\right). \]
显然,等式右边就是常见的分类任务的损失函数,其中加号左边可以是BCE、CE这种,加号右边可以是L1、L2正则化。如果按照优化的思路,找到一个神经网络的参数\(x\)使得 \(-\log{p(x|\mathcal{D}_{train})}\)
最小,我们就找到了当前训练集上的一个最优模型,神经网络的推理过程就是再次计算似然函数:
\[ p(d_{test}|\mathcal{D}_{train}) = p(d_{test}|x^*), \quad \text{where} \quad x^* = \arg\min_{x} -\log{p(x|\mathcal{D}_{train})}. \tag{4} \]
然而对于贝叶斯学习,或者说贝叶斯推理,推理过程被建模为:
\[ \begin{align*} \begin{split} p(d_{test}|\mathcal{D}_{train}) & = \int \underbrace{p(d_{test}| x)}_{prediction} \frac{\overbrace{p(\mathcal{D}_{train}|x)}^{likelihood}\overbrace{p(x)}^{prior}}{\underbrace{p(\mathcal{D}_{train})}_{marginal}}\mathrm{d}x \\ & = \int \underbrace{p(d_{test}|x)}_{prediction}\underbrace{p(x|\mathcal{D}_{train})}_{posterior}\mathrm{d}x \\ & = \mathbb{E}_{x \sim p(x|\mathcal{D}_{train})}\left[p(d_{test}|x)\right]. \end{split} \tag{5} \end{align*} \]
对比式\((4)\)和\((5)\),可以发现前者取当前训练集的最优的一个模型推理输出概率,而后者计算输出概率关于模型后验分布\(\mathbb{E}_{x \sim p(x|\mathcal{D}_{train})}\)的期望(当然也可以计算方差,建模输出结果的不确定度)。
这就是很多论文提到的:
- 贝叶斯学习(推理)体现了模型输出的不确定度:单个预测结果\(\to\)预测结果的分布
- 贝叶斯学习在少样本情况下不容易过拟合(此时贝叶斯学习的行为类似于集成学习,但一个显著的区别是,若损失函数的surface是凸的,那么集成学习的所有优化点都会坍缩到全局最优,但是贝叶斯学习的分布不会坍缩为狄拉克分布)。
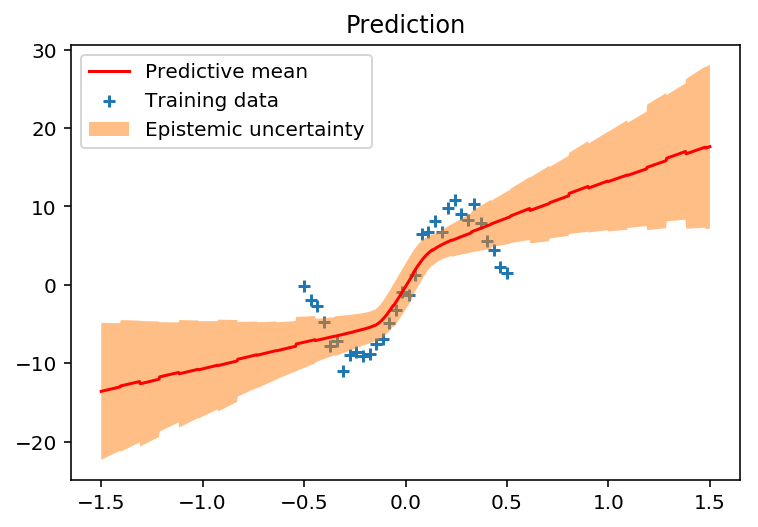
上图是贝叶斯推理处理回归任务的一个简单示例,其中蓝色的点表示训练数据,红色的实线表示预测的平均值,橙色部分表示预测的方差(也是预测结果的不确定度)。可以看到,训练数据稀疏处预测不确定度较大,而训练数据密集处预测的不确定度较小。如果是一般的优化方法,则只有红线部分,没有橙色的预测不确定度部分(给定输入数据,一个模型只能给出一个预测结果)。
采样问题
如何计算贝叶斯推理\((5)\)?
贝叶斯推理的目标计算式为:
\[ p(d_{test}|\mathcal{D}_{train}) = \mathbb{E}_{x \sim p(x|\mathcal{D}_{train})}\left[p(d_{test}|x)\right], \]
其中模型参数的后验分布 \(p(x|\mathcal{D}_{train})\) 与似然函数\(p(d_{test}|x)\)都是由神经网络建模的,意味着我们无法直接得到这个期望式的闭解(积分无法直接计算)。一个可行的替代方案是将求期望近似为采样+求平均:
\[ p(d_{test}|\mathcal{D}_{train}) \approx \frac{1}{M}\sum^M_{i=1}p(d_{test}|x_i), \quad where \quad x_i\sim p(x|\mathcal{D}_{train}). \]
显然\(p(d_{test}|x_i)\)部分是可以计算的,这就是神经网络的forward过程,所以剩余的问题是如何从分布\(p(x|\mathcal{D}_{train})\)采样得到样本点\(x_i\)。这部分的难点在哪里呢?首先我们并不知道完整的概率密度函数\(p(x|\mathcal{D}_{train})\),我们只能拿到一个正比的结论:
\[ p(x| \mathcal{D}_{train} ) \propto \prod^N_{j=1}{p( d_{train, j} |x)}p(x), \]
这是因为边缘归一化参数 \(p(\mathcal{D}_{train})\) 无法计算。其次,在只能拿到概率密度(和其梯度)的条件下,如何对这个分布采样?简单的高斯分布、beta分布等可以非常方便地调用现有的api得到样本点,但是 \(p(x| \mathcal{D}_{train} )\) 显然不属于这种情况。
- 可以通过求积分的方式采样吗?No,\(p(x| \mathcal{D}_{train})\)形式复杂无法求积分
- 可以使用
拒绝采样算法求解吗?No,我们无法得知\(p(x| \mathcal{D}_{train})\)的最大值 - 可以使用
重要性采样算法求解吗?理论上是可以的,但是我们不知道分布\(p(x| \mathcal{D}_{train})\)的“形状”,无法构建合理的参考分布
此时再回顾分布近似问题的定义:
\[ \min_{\mu} \mathcal{F}(\mu, \nu), \]
我们实际上想得到一个粒子点集合(或者说离散经验分布)\(\tilde{\mu} = \{x_i\}^M_{i=1}\),使其尽可能接近目标分布 \(\nu=p(x| \mathcal{D}_{train})\)(先忽略度量\(\mathcal{F}\)的具体定义)。关于该问题,通常有如下三种求解方案(这些方法都需要计算\(p(x| \mathcal{D}_{train})\)的梯度,不过这一项是很好求解,一般可以通过反向传播计算):
- 马尔科夫链蒙特卡洛(MCMC),尤其是2011年后发展的动力学MCMC方法
- 基于模型的变分推理(VI)
- 粒子变分推理(ParVI)
- Bayesian Learning via Stochastic Gradient Langevin Dynamics
- Auto-Encoding Variational Bayes
- Stein Variational Gradient Descent: A General Purpose Bayesian Inference Algorithm
其中:
- VI参数化一个简单分布(比如高斯分布的均值和方差),将原优化变量\(\mu\)改为优化高斯分布的均值和方差,得以在实向量空间求解。在优化结束后,从这个简单的高斯分布抽取样本构建样本点集\(\tilde{\mu} = \{x_i\}^M_{i=1}\)。
- 由于简单分布结构上通常不足够灵活,VI方法的近似结果通常比较“粗糙”。ParVI则直接建模粒子点集\(\tilde{\mu} = \{x_i\}^M_{i=1}\)中每个粒子的位置,然后直接同时优化所有粒子点的位置,使粒子群近似目标分布。
- MCMC有三种形态:
- 随机初始化一个粒子点,然后该粒子点按照某个规律做随机运动,搜集粒子点的运动轨迹,该轨迹的粒子点集合就是目标分布的采样结果
- 随机初始化一群粒子点,这群粒子点按照某个规律做随机运动,迭代若干次后的粒子群状态即为目标分布的采样结果
- 第一种和第二种形态可以混合使用
这里不详细讲三种算法的详细方案,可以参考上述论文或后续章节
三种算法的特性分别为:
- VI基于优化的方法,收敛快,扩展性好(优化结束后可生成任意多的样本点),但是近似精度低。
- ParVI同样基于优化方法,收敛快,近似精度高(粒子数量少的情况下通常远高于MCMC和VI),但是扩展性低(优化结束后无法再增加粒子点),单次迭代的计算复杂度高。
- MCMC基于随机游走,收敛慢,扩展性好,近似精度随着粒子点数量的增加而增加,但在少量粒子情况下精度差(随机性太高)。

上图是一个ParVI迭代过程(从左至右)的典型示例(二维分布近似),我将粒子点标上了颜色,可以更清楚观察到粒子点的移动轨迹。背景的等高线表示目标分布的概率密度。
生成模型
采样问题的设定中,目标分布\(\nu\)是连续分布,对空间中的点\(x\)可计算该处的概率密度函数\(\nu(x)\)。而分布近似问题的另一种设定,目标分布为离散经验分布(用\(\tilde{\nu}\)表示),此时目标分布的概率密度函数不可知,\(\tilde{\nu}\)表示为\(N\)个粒子点\(\{y_j\}^N_{j=1}\)(有权重的情况下表示为\(\{(\beta_j,y_j)\}^N_{j=1}\)),此时分布近似问题可看作以度量\(\mathcal{F}\)为损失函数的拟合问题。
分布近似问题与生成模型的联系是什么?
以CV的生成模型为例,这些模型的目标是将随机的高斯噪声样本\(z\)转化为图像\(\tilde{x}\),并且希望生成的图像\(\tilde{x}\)接近真实图像\(x\)。我们假设模型参数可以用符号\(\theta\)表示,由网络参数化的“生成”分布可表示为\(p_\theta(x)\)。总而言之,这些符号的意义如下:
- \(\tilde{\nu}\)表示目标分布,也就是训练的数据集,包含了多张真实图像。
- 随机高维噪声用\(z\)表示。
- 神经网络的参数用\(\theta\)表示,随机噪声\(z\)可以通过神经网络转化为图像\(\tilde{x}=f_\theta(z)\)。
- 由神经网络参数化的“生成分布”表示为\(p_\theta(x)\)。
这里有一点符号混淆的问题是我们同时用\(x\)表示实向量空间中的点以及真实图像,而用\(\tilde{x}\)仅表示生成图像,但是应该比较好理解。
什么是参数化的“生成分布”呢?这里生成网络的作用是将高斯分布的噪声转化为图像,也就是说生成的图像实际上来自于某个未知的分布,由于大多数的神经网络(除了特殊设计的Flow Model)是不可逆的,这个生成的分布无法计算概率密度函数,我们能得到的仅仅只有通过神经网络生成的“真实”图像样本。这里仅仅是把这个未知分布用数学符号\(p_\theta(x)\)表示。
接下来我们以VAE(变分自编码器)为例,介绍如何推导出VAE的优化目标。首先我们从分布近似问题的定义出发:
\[ \min_\theta{\mathcal{F}(p_\theta, \tilde{\nu})}, \]
上式表达的意思是:优化一个神经网络,使得网络参数化的分布\(p_\theta\)接近目标分布\(\tilde{\nu}\)(真实图像),进而使生成的图像接近真实图像。具体来说,VAE使用的度量\(\mathcal{F}\)是\(KL\)散度:
\[ \begin{align*} &\min_\theta{KL(\tilde{\nu} \| p_\theta)}\\ \Rightarrow & \min_\theta \int{\log{\frac{\tilde{\nu}}{p_\theta}}\mathrm{d}\tilde{\nu}} \\ \Rightarrow & \max_\theta \int{\log{p_\theta}\mathrm{d}\tilde{\nu}} \\ \Rightarrow & \max_\theta \mathbb{E}_{x \sim \tilde{\nu}}\left[\log{p_\theta(x)}\right], \end{align*} \]
上式就是VAE(也包括了早期的diffusion model)使用的“极大似然”损失函数(优化目标)。
关于\(\log{p_\theta(x)}\),进一步可得:
\[ \begin{align*} p_\theta(x) &= \int{p_\theta(x|z)p(z)\mathrm{d}z} \\ &= \frac{p_\theta(x|z)p(z)}{p_\theta(z|x)}\\ &= \frac{p_\theta(x|z)p(z)q_\phi(z|x)}{p_\theta(z|x)q_\phi(z|x)} \end{align*} \]
这里的\(q_\phi(z|x)\)和\(p_\theta(z|x)\)的含义相似,可以看作是不同神经网络参数化的后验分布。熟悉VAE的读者应该可以看出\(p_\theta(z|x)\)是“未知的”编码器,\(q_\phi(z|x)\)是实际使用的近似编码器,\(p_\theta(x|z)\)是解码器。
对等式两边求对数可得:
\[ \begin{align*} \log{p_\theta(x)} &= \log{\frac{p_\theta(x|z)p(z)q_\phi(z|x)}{p_\theta(z|x)q_\phi(z|x)}} \\ &= \log{\frac{p_\theta(x|z)p(z)}{q_\phi(z|x)}} - \log{\frac{p_\theta(z|x)}{q_\phi(z|x)}} \end{align*} \]
等式两边乘\(q_\phi(z|x)\)然后对\(z\)求积分可得:
\[ \begin{align*} \int{q_\phi(z|x)\log{p_\theta(x)}\mathrm{d}z} &= \int{q_\phi(z|x)\log{\frac{p_\theta(x|z)p(z)}{q_\phi(z|x)}}\mathrm{d}z} - \int{q_\phi(z|x)\log{\frac{p_\theta(z|x)}{q_\phi(z|x)}}\mathrm{d}z} \end{align*} \]
注意到\(\log{p_\theta(x)}\)与积分变量\(z\)无关,可得:
\[ \begin{align*} \log{p_\theta(x)} &= \int{q_\phi(z|x)\log{\frac{p_\theta(x|z)p(z)}{q_\phi(z|x)}}\mathrm{d}z} - \int{q_\phi(z|x)\log{\frac{p_\theta(z|x)}{q_\phi(z|x)}}\mathrm{d}z}\\ &= \underbrace{\mathbb{E}_{z\sim q_\phi(z|x)}\left[\log{\frac{p_\theta(x|z)p(z)}{q_\phi(z|x)}}\right]}_{ELBO} + KL\left(q_\phi(z|x) \| p_\theta(z|x)\right), \end{align*} \]
上述过程就是ELBO(Evidence Lower BOund)的数学推导,注意到KL散度的结果一定是非负的,因此有:
\[ \log{p_\theta(x)} \geq \mathbb{E}_{z\sim q_\phi(z|x)}\left[\log{p_\theta(x|z)p(z) - \log{q_\phi(z|x)}}\right] \]
整理公式,可得如下的优化目标:
\[ \max_{\theta, \phi} \mathbb{E}_{x\sim \tilde{\nu}}\left[ \mathbb{E}_{z\sim q_\phi(z|x)}\left[\log{p_\theta(x|z)p(z) - \log{q_\phi(z|x)}}\right] \right] \]
实际上,VAE和diffusion model的优化目标就是上式,VAE用神经网络建模编码器\(q_\phi(z|x)\),用一个神经网络建模解码器\(p_\theta(x|z)\),diffusion用随机过程建模编码器,并且将解码过程建模为多步神经网络的forward过程。
那么生成对抗网络GAN也可以表达成类似的形式吗?
在2014年发表的最初的GAN论文中可以找到作者对GAN优化目标的数学理解,实际上,GAN最小化参数分布\(p_\theta\)和目标分布\(\tilde{\nu}\)之间的\(JS\)散度(假设判别器以训练到最优):
\[ \min_\theta KL\left(\tilde{\nu} \left\| \frac{\tilde{\nu} + p_\theta}{2} \right. \right) + KL\left(p_\theta \left\| \frac{\tilde{\nu} + p_\theta}{2} \right. \right). \]
除了Vanilla GAN,还有Wasserstein-GAN,MMD-GAN,Sinkhorn-GAN等等,这些都可以用:
\[ \min_\mu{\mathcal{F}(\mu, \tilde{\nu})} \]
表达,区别在于生成分布\(\mu\)的定义形式和使用的度量\(\mathcal{F}\)不同。
- Wasserstein GAN
- MMD GAN: Towards Deeper Understanding of Moment Matching Network
- Learning Generative Models with Sinkhorn Divergences
最后,粒子变分推理法可以直接计算离散经验分布\(\tilde{\mu}\),使其近似真实图像分布\(\tilde{\nu}\)。这个过程可以没有网络,ParVI可以直接计算出每个噪声平滑地变换为图像的过程,当然也可以用神经网络拟合这个过程,这也是2022年末很多diffusion模型的做法,这里我们不讨论详细的数学过程。
代码可参考:https://github.com/lzj-isee/dpvi_discrete。

上图是ParVI方法在cifar10数据集上的一个简单实验结果。